ブラックジャックの戦略に役立つ確率と計算方法を解説|基礎と応用
ブラックジャックは、バカラやポーカーに並ぶ人気カジノゲームの一種で、「期待値」が高いことでも有名です。 特に確率的判断能力が求められるブラックジャックでは、確率の知識を蓄えて実践で活用できれば、確実に他のゲームより勝てるようになります。
本記事では、ブラックジャックの戦略に役立つ大切な確率と計算方法を詳しく解説します。
- ブラックジャックの確率を知る前に大切な基礎知識
- ブラックジャックの初心者が覚えておきたい基本的な3つの確率
- ブラックジャックの実践で判断材料を増やすための上級者向けの確率
目次[閉じる]
ブラックジャックの確率を知る上で大切な基礎知識

ブラックジャックの確率は、ゲーム戦略上、非常に大切な知識です。
他カジノゲームと比べて、ブラックジャックはプレイヤーの判断が結果に影響されやすく、その判断の精度はおおよそ確率の知識で決まります。
つまり、ブラックジャックの確率を深く理解することで確実に強くなれるというわけです。また、ブラックジャックは正確な確率に基づいてアクションを選択できれば、期待値1以上でプレイできる唯一のカジノゲームです。
ここではブラックジャックの確率を詳しく紹介しますが、前提として以下2点を覚えておきましょう。
参考:ブラックジャック完全ガイド|基本ルールや攻略法を初心者向けに解説
実際の確率は常に変動している
ブラックジャックの各種確率は常に変動しています。
ブラックジャックは通常ジョーカーを除く計52枚のトランプを6デッキから8デッキ使用します。そして一度、使用したカードはデッキに戻さずディスカードホルダーに捨てます。
つまり、一度テーブルに配られたカードの枚数や種類によって、デッキ(未使用)には偏りが発生します。
例えば次に「5」を引く確率は、現時点の未使用デッキのカード枚数と、デッキ内に残っている「5」の枚数で以下のように変動します。
| 現時点 | デッキ内の合計枚数 | デッキ内の5枚数 | 5の出現確率 | |
|---|---|---|---|---|
| Case1 | 開始時 | 312枚 | 24枚 | 約7.69% |
| Case2 | 中盤戦 | 160枚 | 7枚 | 約4.37% |
上記から分かるように、ブラックジャックの確率は、「どの時点も常に同じカード(数字)が平均的に使用」されていることが前提となるので、実践では「カードの偏り」を把握しながらプレイする必要があります。
ブラックジャック戦略に確率を応用する際の考え方
ブラックジャックの実践に確率を応用する際、プレイヤーはカード2枚が配られた瞬間に自分のハンドとディーラーのアップカードから以下2通りの有利な方を考えます。
- カードの合計をディーラーより「21」に近づけて勝利
- カード合計を「21」に近づけるのは諦めてディーラーにバーストさせて勝利
確率に基づき、有利な方向性に当てを付けて、その方向で勝利する戦略を立てます。以下はブラックジャックの実践例と考え方です。
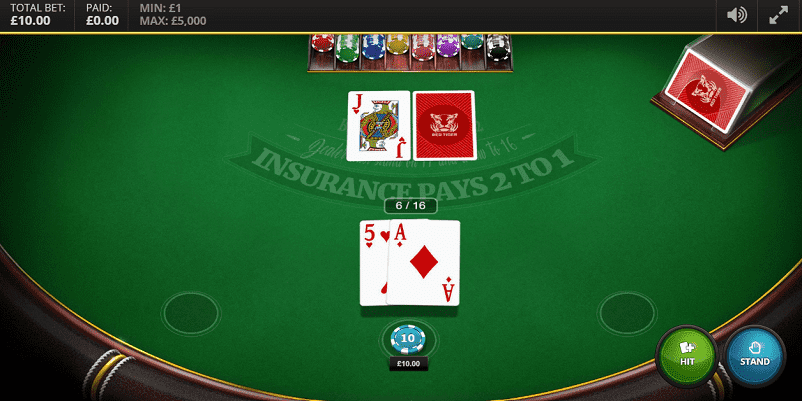
プレイヤーに配られたカード2枚の合計「16」または「6」でディーラーのアップカードは「10」です。
この状況では、プレイヤーが3枚目を引いてもバーストする可能性は無く、ハンドの合計がより21に近づく可能性は約38%です。
一方、ディーラーのダウンカード(裏向き)が「10」の可能性は約30%、さらに17以上になる可能性は53%以上となります。つまり、ここでプレイヤーはスタンドすると、53%以上の確率で負けが決定します。また、ヒットをしてもバースト確率は0%、更に38%以上の確率で合計21に近づくので、合理的な選択としては「HIT(ヒット)」となります。
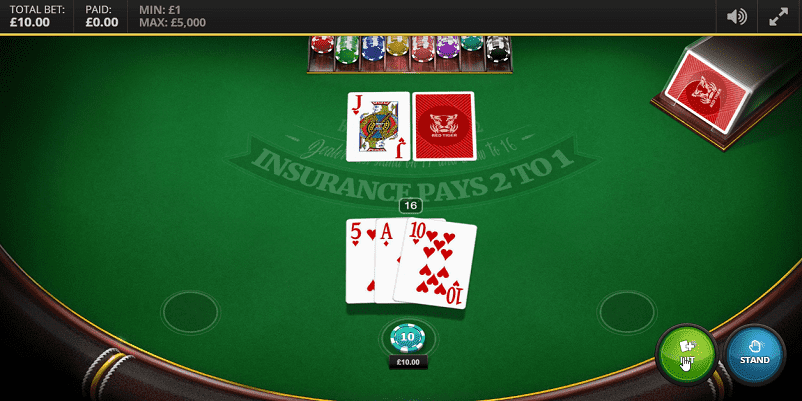
プレイヤーの3枚目は「10」なので、ハンドの合計16となりました。対するディーラーのアップカードは「10」です。
ここの判断方法は以下のようになります。
プレイヤーはスタンドして勝つ方法は、ディーラーのバーストしかありません。そして現時点でディーラーのバースト確率は約21%程度、合計17以上になる確率は約53%になります。
プレイヤーがヒットすると、合計21を超えてバーストの確率は約61%、合計21に近づく可能性は約39%となります。
この確率を踏まえて、プレイヤーはヒットすると約61%の確率でバーストして負けますが、スタンドしても53%の確率で負けます。ただ、ヒットするば約39%の確率で合計21に近づけて勝てる可能性があるので、合理性の高い「HIT(ヒット)」をします。
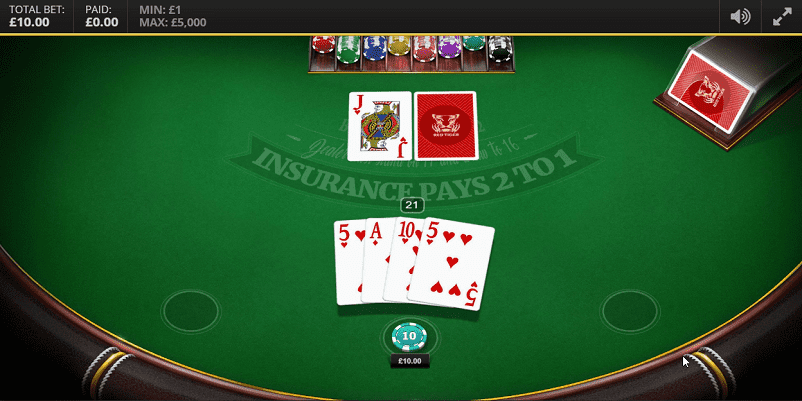
プレイヤーの4枚目のカードは5で合計21となり、最強のハンドとなりました。後は、ディーラーのダウンカードを待つのみです。
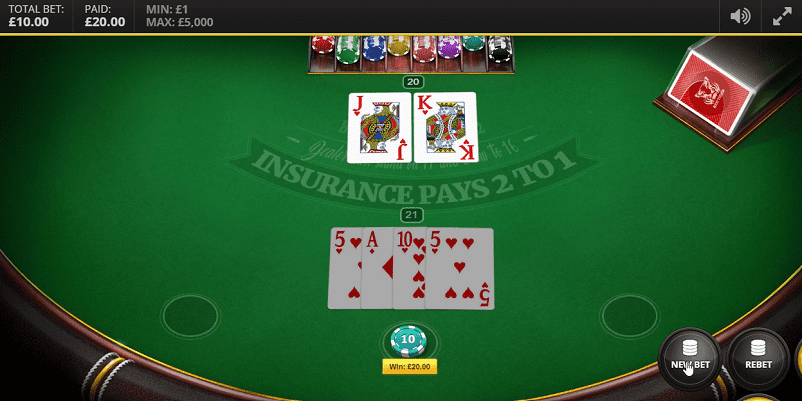
ディーラーのダウンカードは「10」なので合計20となり、プレイヤーの勝利です。このような確率思考に基づいた戦略・判断に必要な確率を以下で紹介します。
ブラックジャック初心者が知っておくべき3種類の確率

ブラックジャックは、重要度の低い確率から高い確率まで様々なケースの確率が計算されています。ここではブラックジャック初心者が覚えておきたい3種類の基本確率を紹介します。
特定のカードを引く確率
ブラックジャックの最も基本的な確率は、次に出現するカードの確率です。特にプレイヤーが次に配られるカードを予想する際や、ディーラーのダウンカードを予想する際に有効です。
| カードの数字 | 出現確率 |
|---|---|
| 1~9 | 各数字とも約7.69% |
| 10 | 約30.76% |
ブラックジャックで「10」と数えるカードは、「10・J・Q・K」と他のカードに比べて4倍多く含まれます。従って、ディーラーのダウンカードは常に「10」と考えて戦略を立てるのが定石です。
ナチュラルブラックジャックの出現確率
ナチュラルブラックジャックとは、最初の2枚のカード合計が「21」になることです。このナチュラルブラックジャックの成立する確率はプレイヤーもディーラーも同じで約4.73%です。
ジョーカーを除く、52枚から2枚のカードを引く組み合わせは全部で1,326通り(5C2=52×51/2)。その中でナチュラルブラックジャックとなる組み合わせは、マーク違いも考慮して「A+10」「A+J」「A+Q」「A+K」。例えば「A+10」について、Aに4種類のマークと10に4種類のマークがあるので計16通り。これが「A+J」「A+Q」「A+K」のパターンに存在するので16通り×4通りで合計64通り。つまり、2枚のカードを引く全通りの組み合わせ1,326通りをナチュラルブラックジャックの組み合わせ64通りで割ると、約4.73%の確率が導けます。
ブラックジャックのバースト確率
ブラックジャックの実践でプレイヤーとディーラーのバースト確率をもとに、アクションを決める状況は多いので、確実に覚えておきしょう。
プレイヤーのバースト確率
ブラックジャックでは、カードを引いて合計21を超えるとバーストで即負けが決まります。
従って、ヒットやダブルダウンを検討する際には、現時点のハンドでヒットしたときのバースト確率を知っておくことが大切です。
プレイヤーのカード合計が12以上のとき、次のカードを引いてバーストする確率を各ハンドごとに以下の表へまとめます。
| ハンド(手札のカード)の合計 | バースト確率 |
|---|---|
| 12 | 30.79% |
| 13 | 38.48% |
| 14 | 46.17% |
| 15 | 53.86% |
| 16 | 61.55% |
| 17 | 69.24% |
| 18 | 76.93% |
| 19 | 84.62% |
| 20 | 92.31% |
| 21 | 100.00% |
ハンドが11以下のとき、バーストする確率は0パーセントですが、12以上になると最低30%以上のバースト確率が出てきます。上記表からも分かるとおり、ハンドが「15-16」だと、ディーラーがバーストしない限り、勝つことはできず、ヒットしても2回に1回以上の確率でバーストするので、他の確率をもとに検討する必要があります。
ディーラーのバースト確率
ディーラーのバースト確率はアップカード(裏向き)の数字によって決まります。
ディーラーはカード合計が「17以上」になるまで機械的にヒットするので、ヒットする回数に関わらず、アップカードの時点で最終的なバースト確率を計算することができます。
ディーラーのバースト確率をアップカード別に以下表にまとめます。
| アップカードの数字 | 最終的なバースト確率 |
|---|---|
| A | 11.6% |
| 2 | 35.3% |
| 3 | 37.5% |
| 4 | 40.3% |
| 5 | 42.9% |
| 6 | 42.1% |
| 7 | 26.0% |
| 8 | 23.9% |
| 9 | 23.3% |
| 10(JQK含む) | 21.4% |
ディーラーのアップカードが「A」や「7~10」のとき、バースト確率は低くなります。
理由はアップカードが「10」や「A」のとき、ダウンカードが7以上なら合計17以上で強制スタンドとなります。そしてディーラーのダウンカードが7以上の確率は約53%と高く、3枚目を引く可能性は低いので同時にバースト確率も低くなります。
一方、ディーラーのアップカードが「4~6」のときバースト確率は40%以上となるので、プレイヤーはリスクを取らず、守備の姿勢でアクションを決めます。
ブラックジャック実践向け!上級者向けの確率

ブラックジャック初心者と上級者の大きな違いは、適切なアクション選択と予想できる範囲の広さです。ブラックジャックの上級者は、目の前の状況だけでなく、ゲーム展開を予想して一歩先の確率を考えたり、特殊アクションの確率も考えています。
そのために初心者向けの基本確率に加えて以下のような確率が必要となります。
- ブラックジャックでヒットして合計「21」になる確率
- 特殊アクションの条件が満たす確率
- ディーラーの最終ハンドが特定の合計値で終わる確率
それぞれ順に詳しく説明します。
ブラックジャックでヒットして合計「21」になる確率
ブラックジャックのカード合計21は、ナチュラルブラックジャックを除いて最強のハンドです。
ただ、1回以上ヒットして合計3枚以上のハンドで合計21になる確率はプレイヤーとディーラーで異なります。
プレイヤーがヒットして合計21になる確率
プレイヤーはヒットをするたびに合計21になる確率が異なるので、あと1回ヒットをして次で合計21になる確率を紹介します。ヒットして次で合計21になる確率はをハンド別にまとめます。
| ハンド(合計) | 合計21になる確率 |
|---|---|
| 9以下 | 0% |
| 10 | 約7.69% |
| 11 | 約30.76% |
| 12以上 | 約7.69% |
ハンドの合計が9以下の場合、次のカードで合計21になる可能性はありません。
ハンドの合計が「10と12以上」のときは、引くべきカードは違いますが、どのカードも1デッキつき、4種類しかないので確率は同じになります。ただ、ハンドの合計が「11」のときは次に「10・J・Q・K」を引くことで合計21になるので、他のハンドより4倍高くなります。
ディーラーがヒットして合計21になる確率
ディーラーが1回以上ヒットして合計21になる確率は、ヒットの回数に関わらず、アップカードの数字で決まります。以下はディーラーが合計21になる確率をアップカード別にまとめた表です。
| アップカードの数字 | 合計21になる確率 |
|---|---|
| A | 7.78% |
| 2 | 11.80% |
| 3 | 11.47% |
| 4 | 11.12% |
| 5 | 10.82% |
| 6 | 9.72% |
| 7 | 7.41% |
| 8 | 6.94% |
| 9 | 6.08% |
| 10(JQK含む) | 6.08% |
上記の「Aと10」には、ナチュラルブラックジャックになる確率は除外されています。ディーラーのアップカードは小さいカードほど高く、大きいカードになると、確率は下がりますが、誤差は約5-6%程度しかありません。
特殊アクションの条件が満たす確率
ブラックジャックには、条件を満たすことで使用できる以下2つの特殊アクションがあります。
- スプリット(最初の2枚がペアにときに使用可)
- インシュランス(ディーラーがアップカードは「A」のときに使用可)
スプリットは同じ数字のペアが配られたとき、ハンドを2つに分けて倍掛けできるアクションです。またインシュランスは、ディーラーのアップカードが「A」のとき、ナチュラルブラックジャックに対する保険を掛けることができるアクションです。
では、スプリットとインシュランスの条件が揃う確率はどのくらいあるのでしょうか。
スプリットの確率
ブラックジャックで最初配られる2枚のカードがペア(同じ数字)になる確率は約13.12%です。つまり、7~8ゲームに1回程度の割合でスプリットを使えることになります。
カード「1~9」の数字がペアになる組み合わせは54通り。「10・J・Q・K」は全て10として扱うので10のペアは120通りあります。トランプ52枚から2枚を引く組み合わせは1326通りなので、「(54+120)/1326」で計算できます。
スプリットは適切なタイミングで使用すれば、とても有効的なアクションなので、実践で使えるようにしておきましょう。
インシュランスの確率
インシュランスは、ディーラーのアップカードが「A」のとき、賭け金の半分を保険料として追加ベットすることができます。もし、ディーラーがナチュラルブラックジャックになれば、賭け金の3倍が配当として払い戻されますが、外れると保険料は没収されます。
インシュランスの条件が揃う確率は、アップカードに「A」が出る確率なので約7.69%となります。また、インシュランスを賭けて成功する確率は「10」を引く確率なので約30.76%となります。インシュランスの成功確率は低く、成功しても損益は±0になるので、期待値から見るとマイナスになることも覚えておきましょう。
ディーラーの最終ハンドが特定の合計値で終わる確率
ディーラーは合計17以上になるまで必ずヒットをするので、最終ハンドは合計17~21となります。ここではバースト確率を除外してディーラーの最終ハンドの出現確率を紹介します。
| ディーラーの最終ハンド | 出現確率 |
|---|---|
| 17 | 14.58% |
| 18 | 13.81% |
| 19 | 13.48% |
| 20 | 17.58% |
| 21(ナチュラル除く) | 7.36% |
ディーラーの最終ハンドは、バースト確率を除外すると、合計20になる確率が17.58%と最も高く、「17~19」は13%~14%程度となっています。
確率に基づいて開発された「ベーシックストラテジー」とは
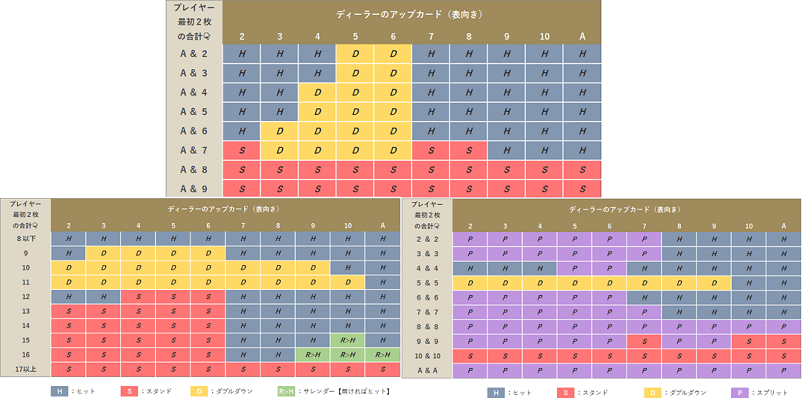
ブラックジャックを楽しむだけなら戦略や確率は不要ですが、本格的に勝ちたいという方は確率と一緒に「ベーシックストラテジー(基本戦略)」も覚えておくことをおすすめします。
ベーシックストラテジーはブラックジャックの基本戦略とも呼ばれており、ストラテジー表を暗記して適切に使用すれば期待値は99%-100%になると言われております。ブラックジャックに強いプレイヤーは、ストラテジー表を覚えてなくても自然に合理的なプレイをしています。ブラックジャックは経験値を積まなくても、ベーシックストラテジーを暗記することである程度、上級者レベルのプレイはできるようになりますので、確率と合わせて覚えることで誰でも勝てるようになります。
ブラックジャックの戦略に役立つ確率のまとめ
本記事では、ブラックジャックの確率を初心者向けと上級者向けに分けて解説しました。
ブラックジャックは、プレイヤーの判断が多く、確率を覚えておくことで精度が高まります。そこで初心者の方は、まず目の前の状況を確率的に判断できるようにしておきましょう。特に以下2種類の確率は、使用する頻度が多く、非常に重要です。
- 特定のカードを引く確率
- バーストする確率
この2点を覚えて使えるようになれば、ブラックジャックの様々な場面で応用できるようになります。
これからブラックジャックを始める方は、まずルールを覚えて確率やベーシックストラテジーの習得に挑戦してみてください。