バカラ編|ココモ法の勝率や期待値を100ゲームで徹底検証
ココモ法は配当3倍以上(勝率33.3%以下)のゲームに使えるカジノ必勝法ですが、意外にバカラのタイ(引分け)に使うプレイヤーは多くいます。当然、配当3倍より高くなればなるほど、ココモ法の効果も低くなるはずですが、なぜ配当9倍にもなるバカラのタイにわざわざココモを使うのでしょうか。
本記事では、バカラでココモ法を使って100ゲームプレイしたときの収支や確率から理由を検証します。
- バカラのタイに賭けたときの基本勝率や期待値
- ココモ法を使ってバカラ100ゲームプレイしたときの勝率や期待値を検証
- バカラでココモ法を使うときのデメリットと改良法
目次[閉じる]
ココモ法の概略と特徴
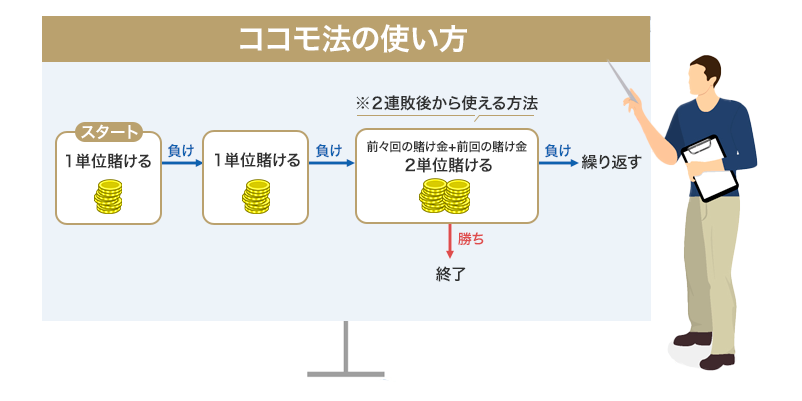
ココモ法は、マーチンゲール法と同様に1度の勝利で連敗中の損失を全額回収できるカジノ必勝法ですが、連敗しても賭け金が高騰しにくく、勝利したときの利益もマーチンゲール法より大きいことが特徴です。
ココモ法は2連敗後から負けるたびに「前々回+前回」ので合計ベット金額を賭けていき、1勝した時点で1セット完了です。連敗数が多ければ多いほど、1勝したときの利益も多くなるので、リスクとリターンのバランスも取れている優秀な必勝法です。
参考:ココモ法とは|使い方や正しい損切り方法とメリット&欠点を解説
ココモ法の使えるバカラの賭け方
ココモ法の使用条件は「配当3倍以上かつ勝率33.3%以下」のベッティングに使用できるので、対象ゲームは限られます。そのためココモ法はルーレットのコラムベットやダズンベットによく使われますが、バカラのタイ(引分け)やペアにも使用されることがあります。
以下はバカラのタイやペアの勝率と配当をまとめた表です。
| 勝率 | 配当 | |
|---|---|---|
| タイ(引き分け) | 9.52% | 9.0倍 |
| プレイヤーペア | 5.88% | 11.0倍 |
| バンカーペア | 5.88% | 11.0倍 |
上記勝率と配当は通常バカラのスペックです。バカラの種類によっては上記の配当倍率や勝率が異なる場合もあるので注意してください。
バカラのタイ(引分け)の主要な理論確率

バカラのタイは、高配当が魅力ですが、勝率が低く、期待値がマイナスなので注意が必要です。バカラでココモ法の威力を検証する前に、バカラのタイ(引分け)の理論勝率や期待値、連敗確率を確認します。
バカラのタイ(引分け)の勝率
バカラのタイ(引分け)の「理論勝率は約9.52%」です。これはプレイヤーとバンカーのハンドが同点になる確率を表しています。
また、バカラはゲームが進むに連れてカードシューの中に偏りが発生するため、常に確率は変動します。
バカラのタイ(引分け)の期待値
期待値とは1回のゲームで賭けた金額に対して受け取れる配当金の平均値です。バカラでタイに賭けた際の期待値をどのくらいの数値になるのでしょうか?
以下はバカラ期待値の計算式です。
期待値=勝率×獲得利益+負ける確率×損失額=0.0952×8+0.9048×(-1)=-0.1432
仮にバカラのタイに100円賭けると、期待値は100×-0.1432=-14.32となります。つまり、100円を賭けると、1ゲーム当たり14.32円の損失が発生することになります。
バカラのタイ(引分け)の連敗確率
バカラでタイに賭けた続けたときの連敗確率を確認します。タイの勝率は9.52%なので、負ける確率は「100%-9.52%=90.48%」です。
この計算をくり返して、連敗する確率を計算すると以下となります。
| 1敗 | 2連敗 | 3連敗 | 4連敗 | 5連敗 | 6連敗 | 7連敗 | 8連敗 | 9連敗 | 10連敗 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 賭け金 | $1 | 1$ | $2 | $3 | $5 | $8 | $13 | $21 | $34 | $55 |
| 勝敗 | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ |
| 累計損失 | -$1 | -$2 | -$4 | -$7 | -$12 | -$20 | -$33 | -$54 | -$88 | -$143 |
| 出現確率 | 90.4% | 81.8% | 74.0% | 67.1% | 60.5% | 54.8% | 49.8% | 45.3% | 41.4% | 37.9% |
バカラのタイへ賭けた場合の連敗確率は7回目のゲームでは、50%を切る49.80%まで減少し、10連敗する確率は37.91%です。逆に言うと、10連敗以内に1勝する確率は62.1%となります。
ココモ法の効果をバカラで実践シミュレーション
バカラのタイ(引き分け)に賭けてココモ法のシミュレーションを行いました。
ここではバカラのタイにココモ法を使って「100ゲーム到達」か「テーブルリミット到達」のどちらが早いか?そして収支も検証します。
ココモ法を使ったバカラ実践結果
ココモ法を使ったバカラのシミュレーション結果を以下表にまとめます。
| 開始時の残高 | £10,000 |
|---|---|
| 終了時の資金 | £7,529(-£2,471減) |
| ゲーム実践時間 | 13分26秒 |
| シミュレーション終了の理由 | 29テーブルリミット到達 |
| 勝敗数(勝率) | 3勝26敗 |
| 最大連敗数 | 16連敗 |
| 瞬間最大利益 | +£110 |
今回のシミュレーションでは29ゲーム目でテーブルリミットに到達しましたが、一時的に£110の利益が出ている状態でした。
ココモ法の有効性を考察|バカラのタイ(引分け)
バカラのタイでココモ法を利用すると、大損失を招くか大きく勝てるか、どちらかということが分かりました。
以下はバカラのタイとココモ法の検証と考察です。
バカラのタイにおける理論勝率は約9.52%ですが、実践シミュレーションでの勝率は29回ベットして3回勝利したため10.5%でした。よって、今回は理論値に対して0.98%高い結果となりました。
今回の実践シミュレーションでは29回ベットしており、合計賭け金は$2,624でした。バカラのタイにおける理論期待値である「-0.1432」をもとに、$2,634ベットした場合の期待値を算出すると、$2,634×-0.1432=「$-377」となりますが、実践シミュレーションでは「$-2,474」と理論上の期待値を大幅に下回っていることがわかります。
今回の実践シミュレーションにおける連敗数は16回でした。理論上、バカラのタイにおいて16連敗が発生する確率は20.8%であり5ゲームに1回は発生する計算となるので、今回のシミュレーション結果は少し運が悪かったといえます。
ココモ法を利用する際、連敗が続く場合は頃合いを見て、損切りをしなければ大敗に繋がることがわかりました。
バカラにココモ法を使用する際のデメリットと改良法

ココモ法の使用条件は「配当倍率3倍以上かつ勝率33.3%未満」なので、当然3倍配当や勝率33.3%前後に賭ける方が効果的です。ただ、バカラには3倍配当となる賭け方が存在しないため、ココモ法の本来の効果を発揮できません。そのため、バカラでは改良ココモ法を使ってパフォーマンスを改善するか、他の「バカラ必勝法」に切り替えるか、どちらかが推奨されます。
そこで、バカラのタイでココモ法の効果を高めるための改良法を紹介します。
タイ(引分け)が9連続で外れるのを待つ
バカラのタイの勝率は約9.5%です。理論上、10回に1回程度はタイが出ることになるので、9回ほど様子を見て、タイが1度も出なければ、次のゲームから参加してタイに賭け続けます。仮に10連敗後に参加して通算15ゲーム目でタイ予想が的中すれば賭け金$1でも$45の配当金を受け取ることができ、4連敗の損失額$12を相殺しても$33の利益が残ります。
また14連敗後の15ゲーム目でタイが出現する確率は約75%となります。比較的確率も高く、高配当を狙えるので1つの戦略として利用すると良いでしょう。
〇倍型ココモ法に改良
バカラの主流な賭け方はプレイヤー・バンカー・タイの3種類ですが、実はサイドベットも存在します。ココモ法を使ってタイに賭ける際はサイドベットも組み合わせることで威力が高まります。
具体的に「配当5倍(勝率約20%)のイーザーペア」で、ココモ法を使う例を紹介します。
イーザーペアとは「プレイヤー」か「バンカー」を決めて、賭けた方の最初2枚のカード(数字)が同じになれば配当を受け取ることができます。
イーザペアの配当倍率は5倍なので、ココモ法も5倍配当型に変形します。5倍型ココモ法は負けるたびに「前ゲーム+2ゲーム前+3ゲーム前+4ゲーム前」の合計金額を賭けていきます。これにより、1回の勝ちでこれまでの損失をすべて回収し、利益も獲得できます。
バカラ×ココモ法の総合的な評価
ココモ法は本来、3倍配当のゲームで使うカジノ必勝法です。
通常、ルーレットのコラムベットやダズンベットで利用されることが多くありますが、3倍配当の賭け方がないバカラでは、9倍配当となるタイでココモ法を使うことができます。しかし、バカラのタイは勝率が10%を切るほど低いため、勝つまでココモ法を続けていると、テーブルリミットに到達する可能性があります。
ただ理論上、バカラのタイは10回に1回程度は出現するので、タイが9回連続で外れたタイミングを見計らってゲームに参加すると理論上は勝つことができるのでオススメです。
また、改良法として配当5倍、勝率20%のイーザーペアで、ココモ法を使うことで弱点を補うことができます。
また、バカラでココモ法を使うなら、事前に目標額を設定しておき、目標到達次第、勝ち逃げするのが吉といえます。長期戦になれば損失が膨らみ、回収困難に陥る可能性があるからです。